4.5 Prueba de hipótesis para diferencia de medias con varianzas conocidas y desconocidas
Ejemplos
1) Un diseñador de productos está interesado en reducir el tiempo de secado de una pintura tapa poros. Se prueban dos fórmulas de pintura; la fórmula 1 tiene el contenido químico estándar, y la fórmula 2 tiene un nuevo ingrediente secante que debe reducir el tiempo de secado. De la experiencia se sabe que la desviación estándar del tiempo de secado es ocho minutos, y esta variabilidad inherente no debe verse afectada por la adición del nuevo ingrediente. Se pintan diez especímenes con la fórmula 1, y otros diez con la fórmula 2. Los dos tiempos promedio de secado muestrales son 121 min y 112 min respectivamente. ¿A qué conclusiones puede llegar el diseñador del producto sobre la eficacia del nuevo ingrediente, utilizando (error, significancia)a = 0.05?
Datos.
𝜎1= 𝜎2= 8
x1= 121 min
x2= 112 min
n1=n2= 10
𝛼= 0.05
Ensayo de hipótesis
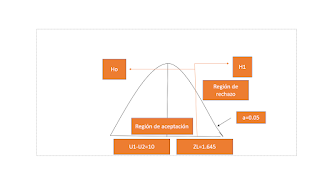
1) Ho; m1-m2 = 0
2) H1; m1-m2 > 0 Se desea rechazar Ho si el nuevo ingrediente disminuye el tiempo promedio de secado, por eso se pone la diferencia mayor a cero o sea positiva para poder probar que m2 es menor que m1.
Regla de decisión:
1) Si zR1.645 no se rechaza Ho.
2) Si zR> 1.645 se rechaza Ho . (esta se
acepta
Fórmula
z = (x1 − x2) −(μ1 − μ2) /√σ12/n1+σ22/n2= (121−112) −(0) /√82/10+82/10= 2.52
2) Se utilizan dos máquinas para llenar botellas de plástico con un volumen neto de 16.0 onzas. Las distribuciones de los volúmenes de llenado pueden suponerse normales, con desviaciones estándar s1= 0.020 y s2= 0.025 onzas. Un miembro del grupo de ingeniería de calidad sospecha que el volumen neto de llenado de ambas máquinas es el mismo, sin importar si éste es o no de 16 onzas. De cada máquina se toma una muestra aleatoria de 10 botellas. ¿Se encuentra el ingeniero en lo correcto? Utilice a = 0.05 (significancia, error)
Datos:
𝜎 1= 0.020
𝜎 2= 0.025
𝑥1 = 16.015 Este dato se obtuvo calculando la media de los datos en la máquina 1.
𝑥2 = 16.005 Este dato se obtuvo calculando la media de los datos en la máquina 2.
n1=n2 = 10
a = 0.05
Ensayo de hipótesis
1 )Ho; m1-m2 = 0
2) H1; m1-m2 ≠0 Si se cae en Ho se podrá
probar que el volumen de llenado es el
mismo en las dos máquinas.
Regla de Decisión:
1) Si –1.96ZR1.96 No se rechaza Ho
2) Si ZR < -1.96 ó si ZR > 1.96 Se rechaza Ho
Fórmula
z = (x1 − x2) −(μ1 − μ2) /√σ12/n1+σ22/n2= (16.015−16.005) −(0) /√0.0202/10 + 0.0252/10= 0.987
3) Existen dos tipos de plástico apropiados para su uso por un fabricante de componentes electrónicos. La tensión de ruptura de ese plástico es un parámetro importante . Se sabe que 𝜎¹= 𝜎²= 1.0 psi. De una muestra aleatoria de tamaño 10 y 12 para cada plástico respectivamente, se tiene una media de 162.5 para el plástico 1 y de 155 para el plástico 2. La compañía no adoptará el plástico 1 a menos que la tensión de ruptura de éste exceda a la del plástico 2 al menos por 10 psi. Con base a la información contenida en la muestra, ¿la compañía deberá utilizar el plástico 1? Utilice a = 0.05 =5%(nivel de significancia /error) para llegar a una decisión.
Datos
𝜎¹= 𝜎² = 1.0 PSI
x1= 162.5 psi
x2= 155 psi
n1= 10
n2= 12
𝛼= 0.05
3. Ensayo de hipótesis
Ho; m1-m2 = 10
H1; m1-m2 > 10 Se desea rechazar Ho si la media del plástico 1 supera a la media del plástico 2 en por lo menos 10 psi.
Regla de decisión:
1) Si zR1.645 no se rechaza Ho.
2)Si zR> 1.645 se rechaza Ho.
Fórmula
z = (x1 − x2) −(μ1 − μ2) /√σ12/n1+σ22/n2= (162.5−155) −(0) /√1.02/10 + 1.02/12= 17.516
EJERCICIOS
1. Se sabe que el contenido en gramos de un producto fabricado por una compañía, no reúne las especificaciones si la varianza de un lote de producción se aleja demasiado hacia arriba o hacia abajo de 6.5. Comprobar si un gran lote de producción reúne las especificaciones, si una muestra aleatoria de 20 unidades extraída aleatoriamente de dicho lote arrojó una varianza de 7.3. Utilizar un nivel de significación (𝛼) del 5%. Se sabe que el contenido del producto se distribuye normalmente.
1) Hipótesis nula e hipótesis alternativa: H⁰⁵., 𝜎²= 6.5 , 𝐻𝑎 = 𝜎² ≠ 6.5
La prueba es bilateral, puesto que el problema es claro en el sentido de que un valor diferente a 6.5 no reúne las especificaciones.
2) Nivel de significación: 𝛼 = 0.05
3) Criterio de decisión: Como la población se distribuye normalmente y la prueba es bilateral, entonces, según las tabla para 19 grados de libertad el valor de y el valor de . Por lo tanto, el criterio de decisión será el siguiente: “Si el valor de calculado es menor que 8.90652 o mayor que 32.8523, se rechaza la hipótesis nula de que la varianza sigue siendo de 6.5, con un nivel de significación del 5%”. Z= 21.34 se acepta la hipótesis nula
4) Cálculo del estadístico sobre el cual se basará la decisión: n=20, S²=7.3. Según l a fórmula 6.15 de la página 175 tenemos:
X²= (n-1) s²/ 𝜎²= (20-1) 7.3/6.5 = 21.34
5) Tomar la decisión: Como el valor de X² calculando (21.34) se encuentra en la zona de aceptación, entonces con un nivel de significación del 5% se acepta la hipótesis nula de que la variable en el contenido sigue siendo la misma, es decir 𝜎 ²= 6.5.
4.6 Prueba de Hipótesis para una varianza
2) La gerencia de una empresa avícola considera que la variabilidad que se presenta en el peso de los pollos de 3 meses es aceptable, puesto que cree que la desviación estándar de los pesos es de 250 gramos. Un grupo de socios de la empresa pone en duda lo manifestado por la gerencia y considera que la variabilidad es superior; por lo cual 6 meses después la gerencia ordena tomar una muestra de 30 pollos de 3 meses seleccionados aleatoriamente y encuentra que la desviación estándar de la misma es de S=225 gramos. Con un nivel de significación del 5%, compruebe quien tiene la razón.
Solución
1) Hipótesis nula e hipótesis alternativa: H⁰:𝜎 = 250, 𝐻𝑎: 𝜎 > 250.L a prueba es unilateral a la derecha, puesto que el grupo de socios considera que la variabilidad es superior a 250 gramos.
2) Nivel de significación: 𝛼 = 0.05
3) Criterio de decisión: Como la población se distribuye normalmente y la prueba es unilateral a la derecha, entonces, según las tablas para 29 grados de libertad el valor de . Por lo tanto, el criterio de decisión será el siguiente: Si el valor de calculado es mayor que 42.5570, se rechaza la hipótesis nula de que la desviación estándar es de 250 gramos.
4) Calculo del estadístico sobre el cual se basará la decisión: n=30, S=135, 𝜎= 225
Fórmula
x2 =(n−1) s2/σ2=(30−1) 135/225= 17.4
4.7 Prueba de Hipótesis para una razón de varianzas
1) Se quiere comprobar si la variabilidad en la duración de unas lámparas marca A es igualmente variable que la duración de otra marca B de la competencia. Para tal fin, se toma una muestra aleatoria de 13 lámparas tipo A y se encuentra que la desviación estándar muestral es S=8, mientras que en otra muestra aleatoria de 13 lámparas tipo B se encuentra que la desviación estándar muestral es de S=4. Se pide probar la hipótesis nula de que la variabilidad es igual en ambas poblaciones con un nivel de significación del 5%. Se supone que la duración de las lámparas se distribuye normalmente para ambas marcas.
Solución
1) Hipótesis nula e hipótesis alternativa para prueba bilateral: H⁰2221:𝜎1² = 𝜎2² y Ha: 𝜎1² ≠ 𝜎2²
2) Nivel de significación:𝛼 = 0.05
3) Criterio de decisión: Si el valor de F calculado se encuentra fuera del intervalo señalado por los dos valores de F según la tabla, entonces rechazamos la hipótesis nula de que las dos desviaciones estándar poblacionales son iguales. Es decir, si el valor de F calculado está fuera del intervalo F(0.025,12,12)=3.28 y F(⁰.⁹⁷⁵, ¹², ¹²) =1/3.28=0.305, entonces se rechaza la hipótesis nula.
4) Cálculo del estadístico sobre el cual se basará la decisión: n¹=13, S¹=8, n²=13,
S²=4:
Fórmula
F= s1²/s2²=4
F=8²/4²=4
5) Decisión: Como 4 se encuentra fuera del intervalo según el criterio de decisión, entonces, con un nivel de significación del 5%, se rechaza la hipótesis nula de que la variabilidad sea igual para ambas marcas.





No hay comentarios.:
Publicar un comentario